Основы технической механики
учебно методический комплекс
понедельник, 18 июня 2018 г.
четверг, 7 июня 2018 г.
Сегодня на уроке
Плоскопараллельное движение твердого тела.
Примером плоскопараллельного движения может служить движение шатуна кривошипно-шатунного механизма. Движение колеса на прямолинейном участке пути. и т.д.
Точку, вокруг которой фигура совершает поворот, называют полюсом.
Плоскопараллельное движение можно разложить на два составляющих движения: поступательное вместе с некоторым полюсом и вращательное вокруг этого полюса
Задача: Вал вращается с угловой скоростью 6 рад/с. После отключения двигателя, его движение стало равномерно замедляться с угловым ускорением е =-0,15 рад/с2. Определите графически и аналитически время, через которое вал остановится (9с).
Задача: Вал вращается с угловой скоростью 6 рад/с. После отключения двигателя, его движение стало равномерно замедляться с угловым ускорением е =-0,15 рад/с2. Определите графически и аналитически время, через которое вал остановится (9с).
четверг, 31 мая 2018 г.
Сегодня на уроке
Поступательное и вращательное движение твердого тела
- Какое движение называют поступательным?
- Какое движение называют вращательным?
- Приведите примеры поступательного и вращательного движения?
- Какой величиной характеризуется вращательное движение?
- Запишите формулу угловой скорости?
- Назовите единицу измерения угловой скорости?
Решите задачи:
Тело начинает вращаться равномерно-ускоренно из состояния покоя, делает 7200 оборотов за первые 2 мин. Определите угловое ускорение (2п рад/с2).
Вал начинает вращаться равномерно-ускоренно из состояния покоя и в первые 5 с он совершает поворот на угол 25 рад. Какова его угловая скорость по истечении 10с? (20 рад/с).
Вал начинает вращаться равномерно-ускоренно из состояния покоя и в первые 5 с он совершает поворот на угол 25 рад. Какова его угловая скорость по истечении 10с? (20 рад/с).
понедельник, 21 мая 2018 г.
воскресенье, 22 апреля 2018 г.
Сегодня на уроке
Деформация кручения. Основные понятия.
Кручение — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил (момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор — крутящий момент. На кручение работают пружины растяжения-сжатия и валы. При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию.
Деформацию кручения можно наблюдать, если на стержень, один конец которого закреплен, действует пара сил, лежащих в плоскости, перпендикулярной оси стержня. При кручении отдельные слои тела остаются параллельными, но поворачиваются друг относительно друга на некоторый угол. Деформация кручения представляет собой неравномерный сдвиг. Деформации кручения возникают при завинчивании гаек, при работе валов машин.
Пример деформации кручения цилиндрического стержня

Если проволоку или стержень, закрепленные с одного конца, закручивать, прилагая к другому концу пару сил F с моментом, равным М, то стержень (проволока) претерпевает деформацию кручения, при которой одно его основание поворачивается по отношению к другому, фиксированному, на некоторый угол φ – угол кручения (рис. 1; 2).
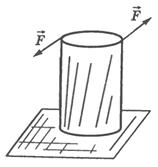
Рис. 1.
Отношение угла закручивания φ к длине  называют относительным углом закручивания
называют относительным углом закручивания
 называют относительным углом закручивания
называют относительным углом закручивания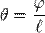
Закон Гука для малых деформаций кручения выражается формулой


 M = Gкр.j
M = Gкр.j
где Gкр.– модуль кручения. 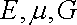



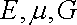



Модуль кручения 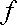

 , помимо материала, зависит также от формы и размеров тела.
, помимо материала, зависит также от формы и размеров тела.
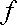

 , помимо материала, зависит также от формы и размеров тела.
, помимо материала, зависит также от формы и размеров тела.
Представьте, перед вами цилиндр (или проволока). Если вы начнёте его (её) верхний конец поворачивать вдоль оси, закрепив нижний конец, то при повороте верхней грани на один радиан вы прикладываете вращающий момент, в точности равный модулю кручения (рис.1; 2). Это и есть его определение.
Модуль кручения Gкр показывает, какой момент силы нужно приложить, чтобы закрутить проволоку на угол в 1 рад.

Рис. 2.
Деформация кручения является частным случаем деформации сдвига.
воскресенье, 1 апреля 2018 г.
пятница, 23 февраля 2018 г.
Продольные силы при растяжении и сжатии. Построение эпюр продольных сил
Пример построения эпюры продольных сил
Задача
Для прямого стержня нагруженного системой внешних сил требуется построить эпюру внутренних продольных сил N.

Решение
В предыдущем пункте решения задачи была определена опорная реакция R в заделке стержня.
Для расчета величины внутренних сил обозначим характерные сечения стержня (B, C, D, K и M).

Заданный стержень имеет 3 силовых участка: BC, CK и KM. Обозначим эти участки римскими цифрами, например, справа налево.
Сечение D, где меняется поперечный размер стержня, границей силового участка не является.
На каждом из этих участков определим величину и знак внутренней продольной силы.
Для этого воспользуемся методом сечений.
Для этого воспользуемся методом сечений.
Начнем с I силового участка (KM):
Проведем мысленно сечение в пределах рассматриваемого участка.

Это сечение делит стержень на две части: левую и правую.
Для упрощения расчетов рекомендуется выбирать ту часть стержня, к которой приложено меньше сил. Очевидно, это будет правая часть стержня (т.к. слева от сечения 4 силы, а справа всего одна).

Внутренняя сила в данном сечении будет равна сумме внешних сил рассматриваемой правой части стержня. С учетом правила знаков при растяжении-сжатии эта сумма будет иметь следующий вид:
Здесь сила F3 записана отрицательной, так как сжимает рассматриваемую часть стержня (направлена в сторону проведенного сечения).
Переходим на второй силовой участок (CK).

Рассекаем стержень в произвольном месте участка и рассматриваем, например левую его часть.
Здесь силы R и F1 положительны, т.к. стремятся растянуть II участок стержня (направлены от сечения).
Аналогично для третьего силового участка (BC)

По полученным данным строим эпюру продольных сил N.

Подписаться на:
Сообщения (Atom)




