Поступательное и вращательное движение твердого тела

Поступательное движение твердого тела

Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.

Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли (рисунок 1.1) и т.д.

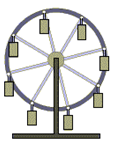
Рис. 1.1

Теорема

При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.

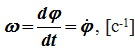
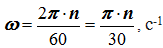
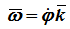
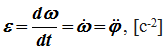
Вращательное движение твердого тела

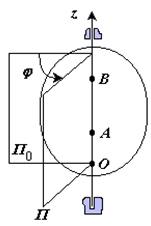
Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φмежду плоскостями П0 и П, одна из которых неподвижна, а другая жестко связана с телом.

φ=φ(t) – уравнение вращательного движения твердого тела.

Рис. 1.3

За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z.

Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.

Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:

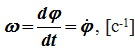
В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим

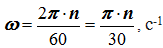
Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости

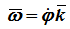
где k – единичный вектор оси вращения.

Угловое ускорение – мера изменения угловой скорости:

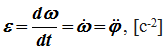
Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)

Рис. 1.4

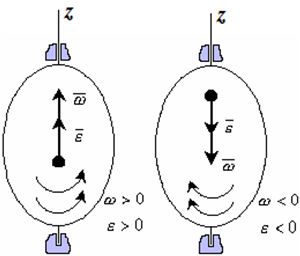
1. Если ε >0 и ω >0 (рисунок 1.4), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов ω и εсовпадают, оба они направлены в положительную сторону оси вращения Oz.
2. При ε <0 и ω <0 – тело вращается ускоренно в отрицательную сторону. Направление векторов ω и εсовпадают, оба они направлены в отрицательную сторону оси вращения Oz.
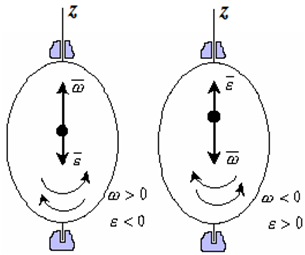
3. Если ε <0 и ω >0, то имеем замедленное вращение в положительную сторону. Векторы ω и ε направлены в противоположные стороны.
4. Если ε >0 при
   ω <0, то имеем замедленное вращение в отрицательную сторону. Векторы ω и ε направлены в противоположные стороны.
5. Если угловая скорость ω=const, то вращательное движение называется равномерным. Уравнение равномерного вращения
   φ=φ0+ωt
6. Если угловое ускорение ε=const, то вращательное движение называется равнопеременным.
   Уравнение равнопеременного вращения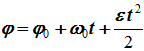и уравнение, выражающее угловую скорость в любой момент времени
   ω=ω0+εt
   представляют совокупность основных формул вращательного равнопеременного движения тела.